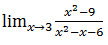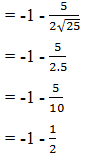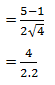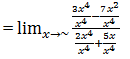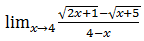Contoh Soal Limit Beserta Pembahasan dan Jawabannya

By Posted on

Assalmu’alaikum wr wb.. Hallo sahabat rumusbilangan.com - kali ini akan kita bahas Pengertian dan Contoh Contoh Soal Limit.

Seperti yang ditulis pada judulnya, didalam artikel ini kita akan lebih banyak memaparkan tentang soal - soal yang berkenaan dengan Limit. Tujuannya untuk lebih memahami dan menghafal cara - cara dalam menggarap soal - soal limit. Untuk itu yuk mari kita simak lebih lanjut!

Pengertian Limit Dalam Ilmu Matematika

Limit didalam konsep ilmu matematik biasa digunakan untuk menjelaskan suatu sifat dari suatu fungsi, saat agumen telah mendekati pada suatu titik tak terhingga atau sifat dari suatu barisan saat indeks mendekati tak hingga.

Limit biasa dipakai dalam kalkulus dan cabang lainnya dari analisis matematika untuk mencari turunan dan kontinyuan.

Pada pelajaran matematika, limit biasanya mulai dipelajari saat pengenalan terhadap kalkulus, dan untuk memahami konsep limit secara menyeluruh bukan sesuatu yang mudah untuk dilakukan.

Limit sebuah fungsi

Apabila f(x) merupakan fungsi real dan c adalah bilangan real, maka bentuk rumusnya yaitu:

{\displaystyle \lim _{x\to c}f(x)=L}

maka sama dengan f(x) dapat dibuat agar mempunyai nilai sedekat mungkin dengan L dengan cara membuat nilai x dekat dengan c.

Pada contoh diatas, limit dari f(x) apabila x mendekati c, yaitu L. Perlu kita ingat, bahwa kalimat sebelumnya berlaku, meskipun f(c) {\displaystyle \neq } L. Bahkan, fungsi pada f(x) tidak perlu terdefinisikan lagi pada titik c. Berikut adalah kedua contoh dibawah ini yang menggambarkan sifat.

Sebagai contoh:

{\displaystyle f(x)={\frac {x}{x^{2}+1}}} pada saat x mendekati nilai 2. Didalam contoh ini, f(x) mempunyai definisi yang jelas pada titik ke-2 dan nilainya sama dengan limitnya, yaitu 0.4:

f(1.9) f(1.99) f(1.999) f(2) f(2.001) f(2.01) f(2.1)
0.4121 0.4012 0.4001 {\displaystyle \Rightarrow } 0.4{\displaystyle \Leftarrow } 0.3998 0.3988 0.3882
Baca Juga :   Pertidaksamaan Nilai Mutlak

Apabila semakin x mendekati 2, maka nilai f(x) mendekati 0.4, dan sebab itu {\displaystyle \lim _{x\to 2}f(x)=0.4}.

Dalam kasus di mana {\displaystyle f(c)=\lim _{x\to c}f(x)}, f disebut kontinyu pada x = c. Namun, kasus ini tidak selalu berlaku. Sebagai contoh:

{\displaystyle g(x)=\left\{{\begin{matrix}{\frac {x}{x^{2}+1}},&{\mbox{if}}x\neq 2\\\\0,&{\mbox{if}}x=2.\end{matrix}}\right.}

Limit g(x) pada saat x mendekat 2 ialah 0.4 (sama seperti f(x), namun {\displaystyle \lim _{x\to 2}g(x)\neq g(2)}: g tidak kontinyu pada titik x = 2.

Atau bisa juga diambil contoh di mana f(x) tidak terdefinisikan pada titik x = c: {\displaystyle f(x)={\frac {x-1}{{\sqrt {x}}-1}}}

Pada contoh ini, pada saat x mendekati 1, f(x) tidak terdefinisikan pada titik x = 1 namun limitnya sama tetap dengan 2, karena semakin x mendekati 1, maka f(x) semakin mendekati 2:

f(0.9) f(0.99) f(0.999) f(1.0) f(1.001) f(1.01) f(1.1)
1.95 1.99 1.999 {\displaystyle \Rightarrow }2{\displaystyle \Leftarrow } 2.001 2.010 2.10

Kesimpulannya:

Maka x dapat dibuat sedekat mungkin dengan 1, asal bukan persis sama dengan 1, oleh karena itu limit darif(x)}{\displaystyle f(x)} ialah 2.

Contoh - Contoh Soalnya

1. Tentukanlah = …

Pembahasannya:


Hasilnya = 6/5

2. Tentukan nilai dari: = …

Pembahasannya:

Kita kerjakan dengan menggunakan rumus:


Maka hasilnya= -3/2

3.Hitunglah pembentukan soal dari = …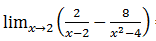
Pembahasannya:


Hasilnya = 2/4
= 1/2

4. Tentukanlah = …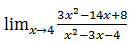
Pembahasannya:


Hasilnya= 10/5
= 2

5. Tentukanlah nilai dari = …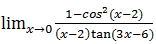
Pembahasannya:

Hasilnya yaitu: 1. 1/3
= 1/3

6. Tentukanlah dari: = …

Pembahasannya:
Kita kerjakan dengan rumus:


= 1

7. Tentukanlah sebuah nilai dari = …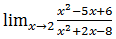
Pembahasannya:


Hasilnya= -1/6

8. Tentukanlah nilai dari = …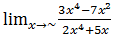
Pembahasannya:


Hasilnya= 3/2

9. Tentukan nilai dari = …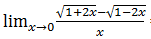
Pembahasannya:


Hasilnya yaitu = 4/2 = 2

10. Tentukan= …

Pembahasannya:


Hasilnya= -1/6

Soal 11: Carilah nilai limit dari berikut ini:

a. lim 4x→3:
b. lim 3xx→3:
c. limx→2
3x2:
d. lim 3x2 + 5x→3:
e. limx→2
2x2 + 42x + 2:

Pembahasannya:

a. lim 4 = 4x→3
b. lim 3x = 3.(3) = 9x→3
c. limx→2
3x2= 3.(2)2 = 3
d. lim 3x2 + 5 = 3.(3)2 + 5 = 32x→3
e. limx→2
2x2 + 42x + 2 = 2.(22) + 42.(2) + 2 = 126 = 2

Soal 12 Hitunglah nilai limit fungsi aljabar berikut:

limx→2

x2 - 4x - 2

Pembahasannya:

Baca Juga :   Rumus Segitiga - Luas, Keliling, dan Contoh Soalnya

Apabila hasil substitusinya adalah 0/0 (bentuk tak tentu), maka cara mencarinya tidak dapat kita lakukan dengan cara memasukkan nilai langsung, melainkan harus difaktorkan terlebih dahulu:

limx→2

x2 - 4x - 2 = 22 - 42 - 2 = (bentuk tak pasti)

Maka hasil faktornya ialah :

limx→2:

x2 - 4x - 2 = (x-2)(x+2)(x-2) = (x+2)= (2+2) = 4

Soal 13: Hitunglah nilai dari limit dibawah ini :

limx→3:

x2 - 9√ x2 + 7 - 4

Pembahasannya:

Dengan substitusi langsung:

limx→3

(x2 - 9)√ x2 + 7 - 4 = (32 - 9)√ 32 + 7 - 4 =

Karena diperoleh bentuk tidak pasti, maka kita harus menggunakan cara lain yaitu menggunakan perkalian akar sekawan:

limx→3

(x2 - 9)√ x2 + 7 - 4 x √x2 + 7 + 4√ x2 + 7 + 4

⇔

limx→3

(x2 - 9).(√x2 + 7 + 4)(x2 + 7) - 16

⇔

limx→3

(x2 - 9).(√x2 + 7 + 4)(x2 - 9)

⇔

limx→3

(√x2 + 7 + 4) = (√32 + 7 + 4) = 8

Soal 14 Hitunglah nilai dari limit fungsi aljabar berikut ini:

limx→2:

x2 - 5x + 6x2 - 4

Pembahasannya:

Apabila disubstitusikan langsung, maka akan didapatkan :

limx→2

x2 - 5x + 6x2 - 4 = 22 - 5.(2) + 622 - 4 = (bentuk tidak pasti)

Maka kita harus menggunakan cara lain, yaitu: dengan mengfaktorkan dan melakukan turunan.

Pada soal no 14 ini kita lakukan dengan turunan :

limx→2

x2 - 5x + 6x2 - 4 = 2x - 52x = 2.(2) - 52.(2) = -14

Soal 15 Tentukanlah nilai limit dari :

limx→∞

4x - 12x + 1

Pembahasannya:

Perhatikanlah pangkat tertinggi dari x pada f(x)= 4x–1 dan g(x)=2x+1.

Ternyata pangkat tertinggi dari x ialah 1.

limx→∞ adalah

4x - 12x + 1

⇔

limx→∞
4xx - 1x2xx + 1x

⇔

limx→∞
4 - 1x2 + 1x

=

4 - 1∞2 + 1∞

=

4 - 02 - 0

= 2

Demikianlah pembahasan kita hari ini mengenai Pengertian Limit dan Contoh-Contoh Soalnya. Semoga bermanfaat …

Baca Juga :   Rumus Belah Ketupat - Luas, Keliling dan Contoh Soalnya

sumber : https://rumusrumus.com/

Baca Juga :

Related posts: