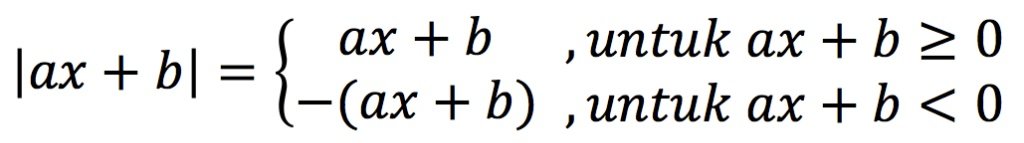RumusBilangan.Com – Pada bab ini, kita akan membahas materi mengenai sistem persamaan nilai mutlak satu variabel beserta contoh soal dan cara penyelesaiannya.

Pengertian Persamaan Nilai Mutlak Satu Variabel
Dalam ilmu geometri, nilai mutlak dari x yang ditulis | x |, ialah suatu jarak dari x ke 0 pada garis bilangan real. Karena jarak tersebut selalu positif atau nol, maka nilai mutlak x juga selalu bernilai positif atau nol untuk setiap x bilangan real.
Nilai mutlak yaitu suatu nilai yang selalu bernilai positif dengan simbol: .
Secara umum, nilai mutlak ini dapat dijabarkan yaitu sebagai berikut:
Selain persamaan di atas, apabila dalam sebuah bentuk aljabar maka dapat kita dapatkan sebuah persamaannya yaitu sebagai berikut:
Konsep Nilai Mutlak
Konsep dari nilai mutlak ini, dapat kita pahami dengan kita perhatikan contoh berikut:
Seorang pemimpin regu PBB pramuka memerintah untuk maju 4 langkah kedepan, maka jarak pergerakan barisan tersebut sebesar 4 langkah ke arah depan, apabila pemimpin barisan memerintah untuk mundur 3 langkah ke belakang, maka jarak pergerakan barisan tersebut sebesar tiga langkah ke arah belakang. Besar pegerakan barisan diatas adalah contoh dari nilai mutlak.
Apabila di gambarkan kedalam bentuk garis bilangan, maka dapat kita lihat sebagai berikut:

Berdasarkan gambar garis bilangan diatas, posisi x =0 adalah merupakan suatu titik awal barisan, kemudian anak panah merah adalah merupakan sebuah pergerakan maju 3 langkah kedepan (mengarah sumbu x positif atau +3) dan untuk anak panah biru adalah merupakan pergerakan mundur 2 langkah ke belakang (mengarah sumbu x negatif atau -2). Sehingga banyaknya langkah pada barisan tersebut adalah merupakan suatu konsep dari nilai mutlak yaitu |3| +|- 2|= 3+2 = 5.
Persamaan Nilai Mutlak Linear Satu Variabel
Dalam sebuah persamaan nilai mutlak linear satu variabel, garis bilangan digunakan untuk media yang berfungsi menunjukan nilai mutlak. Besar nilai mutlak tersebut dapat dilihat dari panjang tanda panah dan dihitung dari nilai nol.
Sedangkan tanda panah digunakan untuk menentukan suatu besaran dari nilai mutlak, dimana arah ke kiri menandakan nilai mutlak dari bilangan negatif, dan begitu juga sebaliknya. Sedangkan arah yang ke kanan menandakan nilai mutlak dari bilangan positif.
Perhatikanlah gambar garis bilangan dibawah berikut:
Pada tanda panah diatas, kita lihat bergerak dari bilangan 0 ke arah kanan menuju bilangan ke 3. Sehingga besar langkah yang dilalui tanda panah diatas adalah 3 (berjarak 3 satuan dari bilangan 0). Hal ini berarti nilai mutlak tersebut adalah |3|= 3
Pada tanda panah diatas, bergerak dari bilangan 0 ke arah kiri menuju bilangan ke 3. Sehingga besar langkah yang dilalui tanda panah tersebut adalah 3 (berjarak 3 satuan dari bilangan 0). Berdasarkan keterangan tersebut, berarti nilai mutlak adalah |-3|= 3
Berdasarkan penjelasan diatas, nilai mutlak ini dapat disebut juga sebagai besaran suatu jarak perpindahan dari titik awal.
Persamaan Dan Pertidaksamaan Nilai Mutlak
Nilai mutlak x ialah suatu jarak dari x ke nol pada garis bilangan real. Dengan definisi ini, solusi dari persamaan dan pertidaksamaan nilai mutlak dari suatu bentuk linier akan kita temukan.
Misalkan: | x | = a dengan a > 0
Persamaan | x | ialah = a yang artinya jarak dari x ke 0 sama dengan a. Perhatikanlah gambar garis bilangan berikut:
Dari gambar diatas, dapat kita pahami bahwa, arah -a ke 0 sama dengan jarak a ke 0, yaitu a. Pertanyaannya yaitu dimana x agar jaraknya ke 0 juga sama dengan a.
Posisi x ditunjukkan oleh titik merah pada gambar diatas, yakni x = -a atau x = a. Yang mana terlihat bahwa jarak antara titik tersebut ke 0 adalah sama dengan a. Maka, agar jarak x ke nol sama dengan a, haruslah x = -a atau x = a.
| x | < a untuk a > 0
Pertaksamaan | x | < a, yang mana artinya jarak dari x ke 0 kurang dari a.
Mari kita perhatikan gambar berikut:
Berdasarkan gambar ilustrasi diatas, dapat dipahami bahwa posisi x ditunjukkan oleh ruas garis yang berwarna merah, yaitu himpunan titik-titik diantara -a dan a yang biasa kita tulis -a < x < a. Apabila kita ambil sebarang titik pada interval tersebut, maka dapat dipastikan jaraknya ke 0 adalah kurang dari a. Maka, agar jarak x ke 0 kurang dari a, haruslah -a < x < a.
| x | > a untuk a > 0
Pertaksamaan | x | > a adalah suatu jarak dari x ke 0 lebih dari a.
Mari kita perhatikan gambar berikut ini:
Berdasarkan gambar ilustrasi di atas, posisi x ditunjukkan oleh ruas garis berwarna merah yaitu x < -a atau x > a. Maka, apabila kita ambil sebarang titik pada interval tersebut, sudah dipastikan jaraknya ke 0 lebih dari a. Sehingga, agar jarak x ke nol lebih dari a, haruslah x < -a atau x > a.
Secara intuitif, uraian-uraian diatas dapat kita simpulkan adalah sebagai berikut :
Contoh Soal Dan Pembahasanya
Contoh 1:
Tentukanlah sebuah himpunan penyelesaian dari |3x – 7| = 3
Penyelesaian :
Berdasarkan sifat a :
|3x – 7| = 3 ⇔ 3x – 7 = 3 atau 3x – 7 = -3
|3x – 7| = 3 ⇔ 3x = 10 atau 3x = 4
|3x – 7| = 3 ⇔ x = 5 atau x = 3
Maka, HP = {3, 5}.
Contoh 2:
Tentukanlah himpunan dari |3x – 1| = |x + 4|
Penyelesaian :
Berdasarkan sifat a :
|3x – 1| = |x + 4|
⇔ 3x – 1 = x + 4 atau 3x – 1 = -(x + 4)
⇔ x = 5 atau 4x = -4
⇔ x = 5 atau x = -1
Maka, HP = {-1, 5}.
Demikianlah pembahasan mengenai Persamaan Nilai Mutlak. Semoga bermanfaat …
Baca Juga: