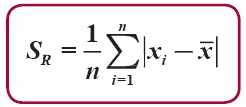Simpangan Rata Rata - Pengertian, Rumus dan Cara Menentukannya. Hallo sahabat rumusbilangan.com- Kali ini kita akan membahas materi tentang Simpangan Rata-Rata yang terdiri dari Pengertian, Rumus dan Cara Menentukannya.

Sebagai intro, saat kita bekerja dengan menggunakan data-data, ada beberapa hal mengenai cara untuk mengukur keseragaman nilai data kita. Cara yang paling umum ialah rata-rata. Kebanyakan orang belajar menghitung rata-rata dengan cara menjumlahkan seluruh nilai data dan membaginya dengan banyaknya data dalam satu set sekaligus.

Terdapat perhitungan tingkat lanjut yakni simpangan rata-rata. Perhitungan ini mengukur seberapa dekat nilai-nilai data yang kita miliki dengan nilai rata-rata kumpulan data tersebut. Caranya, yuk kita simak lebih dalam dibawah berikut:

Daftar Isi Artikel :

Pengertian Simpangan Rata-Rata

Pengertian Simpangan rata-rata atau (deviasi mean) ialah rata-rata jarak antara nilai-nilai data menuju rata-ratanya.

Simpangan rata-rata meripakan termasuk ke dalam ukuran penyebaran data seperti halnya Varian dan Standar Deviasi. Kegunaannya ialah untuk mengetahui seberapa jauh nilai data yang telah menyimpang dari rata-rata yang sebenarnya.

Rumus Simpangan Rata-Rata

Sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x₁, x₂, …, x_n. Dari data tersebut dapat ditentukanlah simpangan rata-rata (S_R) dengan menggunakan sebuah rumus sebagai berikut:

Contoh Soal 1:

Hitunglah simpangan rata-rata dari data kuantitatif berikut :

12, 3, 11, 3, 4, 7, 5, 11

Pembahasan:

Maka, simpangan rata-ratanya ialah 3,25.

Kemudian coba kalian tentukan simpangan rata-rata tersebut dengan menggunakan sebuah kalkulator. Apakah hasilnya juga sama?

Untuk sekumpulan data yang dinyatakan oleh x₁, x₂, …, x_n dan masing-masing nilai data tersebut mempunyai frekuensi f₁ , f₂ , …, f_n maka diperolehlah nilai simpangan rata-rata (S_R) dengan menggunakan rumus:

Contoh Soal 2:

Hitunglah simpangan rata-rata nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka seperti Tabel 1 dibawah berikut:

Tabel 1. Nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka

Interval Kelas	Frekuensi
40 – 44	3
45 – 49	4
50 – 54	6
55 – 59	8
60 – 64	10
65 – 69	11
70 – 74	15
75 – 79	6
80 – 84	4
85 – 89	2
90 – 94	2

Penyelesaian:

Dari tabel diatas, diperoleh = 65,7 (dibulatkan).

Kelas Interval	Nilai Tengah (x_i)	f_i	\|x–x\|	f_i\|x–x\|
40 – 44	42	3	23,7	71,1
45 – 49	47	4	18,7	74,8
50 – 54	52	6	13,7	82,2
55 – 59	57	8	8,7	69,6
60 – 64	62	10	3,7	37
65 – 69	67	11	1,3	14,3
70 – 74	72	15	6,3	94,5
75 – 79	77	6	11,3	67,8
80 – 84	82	4	16,3	65,2
85 – 89	87	2	21,3	42,6
90 – 94	92	2	26,3	52,6
		Σf_i= 71		Σf_i \|x – x\| = 671,7

Maka, simpangan rata-rata (S_R) = 671,7 / 71 = 9,46.

Perlu diingat:

Simpangan rataan hitung tersebut menunjukkan rataan hitung jauhnya datum dari rataan hitung.

Untuk menghitung simpangan baku dari data kuantitatif: 2, 5, 7, 4, 3, 11, 3 dengan kalkulator ilmiah (fx–3600Pv) ialah sebagai berikut:

1)	Kalkulator “ON”
2)	MODE 3 → Program SD
3)	Masukkan data
	2 data
	5 data
	…
	…
	…
	3 data
4)	Tekan tombol x _αn-1
α = 2,878491669 = 2,88

Selanjutnya yaitu membahas Simpangan rata- rata yang dibagi menjadi dua:

Simpangan rata - rata dengan data tunggal
Simpangan rata - rata data berkelompok

1. Simpangan Rata - Rata Dengan Data Tunggal

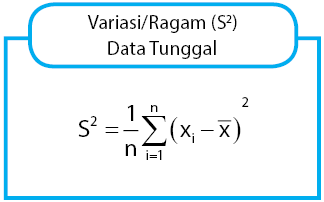
Rumus Variasi $(S^{2})$ dari Data Tunggal

Rumus variasi/ragam dari data tunggal ialah yang dinyatakan melalui persamaan di bawah berikut:

Keterangan:
$x_{i}$ = nilai data ke-i
$\bar{x}$ = rata-rata
n = jumlah seluruh frekuensi

Rumus Standar Deviasi/Simpangan Bakunya Data Tunggal ialah:

Rumus simpangan baku data tunggal dinyatakan melalui sebuah persamaan di bawah berikut:

Keterangan:
$x_{i}$ = nilai data ke –i
$\bar{x}$ = rata-rata
n = jumlah seluruh frekuensi

2. Simpangan rata - rata data berkelompok

Rumus Simpangan Rata-rata (SR) Data Berkelompok ialah sebagai berikut:

Keterangan:
n = jumlah seluruh frekuensi
$f_{i}$ = frekuensi kelas ke-i
$x_{i}$ = nilai tengah kelas ke-i
$\bar{x}$ = rata-rata
k = banyaknya kelas interval

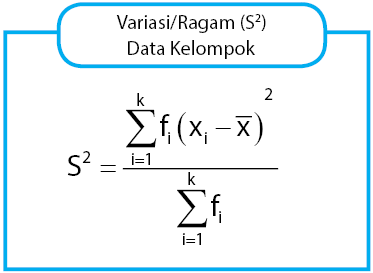
Variasi (Ragam)

Persamaan untuk ragam atau variasi diberkan melalui rumus di bawah berikut:

Keterangan:
$x_{i}$ = nilai tengah kelas ke-i
$f_{i}$ = frekuensi kelas ke-i
$\bar{x}$ = rata-rata
k = banyak kelas interval

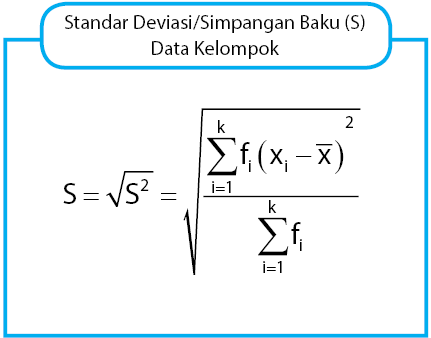
Standar Deviasi (Simpangan Baku)

Rumus simapangan baku untuk data kelompok ialah sebagai berikut:

Keterangan:
$x_{i}$ = nilai tengah kelas ke-i
$f_{i}$ = frekuensi kelas ke-i
$\bar{x}$ = rata-rata
k = banyak kelas interval

Contoh Soal dan Pembahasannya

Diketahui sebuah data terurut $(3x - 3)$ , $2x$ , $(2x + 1)$ , $(3x - 1)$ , $(3x + 3)$ , dan $(4x + 1)$ . Jangkauan data tersebut ialah 6. Simpangan rata-rata data tersebut yaitu …

Pembahasannya:

Diketahui sebuah data terurut ialah sebagai berikut:

$(3x - 3)$ , $2x$ , $(2x + 1)$ , $(3x - 1)$ , $(3x + 3)$ , $(4x + 1)$
Nilai minimum = $x_{min}$ = $3x - 3$
Nilai maksimum = $x_{max}$ = $4x + 1$

$\textrm{Jangkauan} = x_{max} - x_{min}$

$6 = 4x + 1 - \left( 3x - 3 \right)$

$6 = 4x + 1 - 3x + 3$

$6 = x + 4$

$x = 2$

Maka, daftar nilainya yaitu:

$(3x - 3) = 3 \cdot 2 - 3 = 6 - 3 = 3$

$2x = 2 \cdot 2 = 4$

$2x + 1 = 2 \cdot 2 + 1 = 4 + 1 = 5$

$3x - 1 = 3 \cdot 2 - 1 = 6 -1 = 5$

$3x + 3 = 3 \cdot 2 + 3 = 6 + 3 = 9$

$4x + 1 = 4 \cdot 2 + 1 = 8 + 1 = 9$

Oleh karena itu diperolehlah data: 3, 4, 5, 5, 7, 9, 9

Mencari rata-ratanya ialah:

$\bar{x} = \frac{\sum_{i=1}^{n} x_{i}f_{i}}{\sum_{i=1}^{n} f_{i}}$

$\bar{x} = \frac{3 + 4 + 2(5) + 7 + 2(9)}{7}$

$\bar{x} = \frac{42}{7} = 6$

Mencari Simpangan Rata-rata (SR) nya yaitu:

$SR=\frac{1}{n} \sum_{i=1}^{n}\left | x_{i}-\bar{x} \right |$

$SR=\frac{1}{7} \times \left( \left | 3 - 6 \right | + \left | 4 - 6 \right | + 2 \left | 5 - 6 \right | + \left | 7 - 6 \right | + 2 \left | 9 - 6 \right | \right)$

$SR=\frac{1}{7} \times \left( 3 + 2 + 2 \cdot 1 + 1 + 2 \cdot 3 \right)$

$SR=\frac{1}{7} \times \left( 3 + 2 + 2 + 1 + 6 \right)$

$SR=\frac{1}{7} \times \left( 14 \right) = 2$

Demikian lah pembahasan mengenai Simpangan Rata-Rata- Pengertian, Rumus dan Cara Menentukannya. Semoga bermanfaat ya …