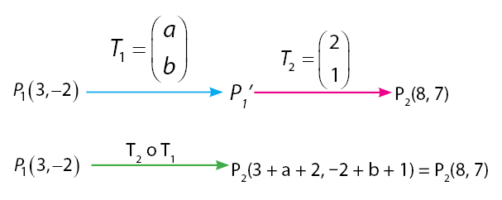Transformasi Geometri - Pengertian, Makalah, Jenis, Contoh Soal

Rumusbilangan.com- Pada bab ini kita akan bahas makalah materi tentang transformasi geometri secara rinci mulai pengertian, jenis, dan contoh soal transformasi geometri.

Pada dasarnya, yang akan kita pelajari pada materi ini adalah materi tentang perubahan karena makna dari transformasi adalah sebuah perubahan dan geometri adalah ilmu yang membahas mengenai bangun.

Maka, dapat disimpulkan bahwa transformasi geometri adalah sebuah proses penentuan titik koordinat baru dari sebuah bangun pada sebuah bidang.

Pada materi ini akan dipelajari mengenai jenis-jenis transformasi dan pengertiannya.

Contents show

Sejarah Transformasi Geometri

Menurut sejarah, materi ini mulai dipelajari ketika seorang ilmuwan yang bernama Felix Klein mengemukakan sebuah teori dalam sebuah paper berjudul Erlangen Program.

Felix Klein mengatakan bahwa geometri adalah sebuah ilmu yang mempelajari tentang bangun yang bisa ditransformasikan ke dalam sebuah bentuk yang berbeda dan sifat-sifat bangun tidak terpengaruh karena perubahan yang dilakukan.

Komposisi transformasi geometri ialah materi yang cukup untuk melatih kemampuan menggambar dan kemampuan matematika kita. Sebab dengan perhitungan matematika yang tepat, kita bisa melakukan sebuah terhadap bangun-bangun yang ada pada matematika ataupun di dalam kehidupan sehari-hari.

Pengertian Transformasi Geometri

Transformasi geometri adalah sebuah perubahan suatu bidang geometri yang meliputi posisi, besar dan bentuknya sendiri.

Apabila hasil transformasi kongruen dengan bangunan yang ditranformasikan, maka dapat disebut transformasi isometri. Sedangkan transformasi isometri sendiri mempunyai dua jenis yaitu transformasi isometri langsung dan transformasi isometri berhadapan.

Transformasi isometri langsung adalah termasuk translasi dan rotasi, sedangkan transformasi isometri berhadapan yaitu termasuk refleksi.

Jenis – Jenis dan Rumus Transformasi

Rumus pada transformasi geometri akan memudahkan kita untuk menentukan sebuah hasil transformasi tanpa harus menggambarnya dalam bidang kartesius terlebih dulu. Meskipun demikian, ilustrasi gambar tentang transformasi juga dapat memberikan sebuah tambahan pemahaman buat kita semua.

Oleh karena itu, yuk kita simak mengenai pembahasan tentang jenis-jenis trasnmorasi yaitu translasi, refleksi, rotasi, dan dilatai pada penjabaran materi di bawah berikut ini.

1. Translasi (Pergeseran)

Translasi adalah perubahan objek dengan cara menggeser objek dari satu posisi ke posisi lainnya dengan jarak tertentu.

Penentuan hasil objek melalui translasi yaitu cukup mudah. Caranya kita hanya dengan menambahkan absis dan ordinat dengan jarak tertentu sesuai dengan ketentuannya. Untuk lebih jelasnya mengenai proses translasi ini, kita dapat mengamati pada gambar di bawah ini.

Refleksi (Pencerminan)

Pencerminan atau yang lebih sering disebut dengan refleksi. Seperti halnya bayangan pada sebuah benda yang terbentuk dari sebuah cermin. Sebuah objek yang mengalami refleksi terebut akan memiliki bayangan benda yang dihasilkan oleh sebuah cermin. Hasil dari refleksi dalam bidang kartesius ini tergantung sumbu yang menjadi cerminnya.

Jenis-jenis tersebut antara lain adalah refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k. Berikut ini ialah ringkasan daftar matriks transformasi pada refleksi/pencerminan.

Rotasi (Perputaran)

Rotasi atau perputaran adalah sebuah perubahan kedudukan objek dengan cara diputar melalui pusat dan sudut tertentu. Besarnya rotasi dalam sebuah transformasi geometri adalahsebesar $\alpha$ disepakati untuk arah yang berlawanan dengan arah jalan jarum jam.

Apabila arah perputaran rotasi suatu benda searah dengan jarum jam, maka sudut yang dibentuk ialah $- \alpha$ . Hasil rotasi pada suatu objek bergantung dari pusat dan besar sudut rotasi.

Perhatikanlah perubahan letak kedudukan segitiga yang diputar sebesar $135^{o}$ dengan pusat $O(0,0)$ pada gambar di bawah berikut:

Dilatasi

Dilatasi atau biasa disebut juga dengan perbesaran atau pengecilan suatu objek. Apabila transformasi pada translasi, refleksi, dan rotasi hanya mengubah posisi benda, maka dilatasi melakukan transformasi geometri dengan merubah ukuran benda.

Ukuran benda tersebut dapat menjadi lebih besar atau lebih kecil. Perubahan ini bergantung pada skala yang menjadi sebuah faktor suatu pengalinya.

Rumus dalam dilatasi ada dua, yakni: yang dibedakan adalah berdasarkan pusatnya. Selanjutnya perhatikan uraian rumus ini untuk sebuah transformasi geometri pada dilatasi di bawah berikut ini:

Contoh Soal Transformasi Geometri

Hasil translasi itik $P_{1}(3, -2)$ dari $T_{1}$ dilanjutkan dengan $T_{2} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}$ menghasilkan titik $P_{2}(8, 7)$ . Komponen translasi dari $T_{1}$ yang sesuai yaitu . . ..