Determinan Matriks - Pengertian, Sifat-Sifat, dan Contoh Soal

Rumusbilangan.com- Materi Cara Menentukan Determinan Matriks Dibahas Lengkap mulai dari pengertian, sifat-sifatnya, dan juga contoh soal determinan matriks beserta pembahasannya.

Hay sahabat,, hari ini kita akan melanjutkan kembali belajar matematika. Kali ini materi yang akan dibahas adalah Bagaimana Cara Menentukan Determinan Matriks, yang meliputi pengertian, sifat-sifat dan beberapa contoh soalnya. Untuk itu yuk kita simak!

Contents show

Pengertian Determinan Matriks

Di dalam bidang materi al jabar linear, determinan ialah sebuah nilai yang dapat dihitung dari unsur suatu matriks persegi.

Determinan matriks $A$ ditulis dengan sebuah tanda, yaitu: $det(A)$ , $det A$ , atau |A|. Determinan bisa dianggap sebagai faktor penskalaan transformasi yang digambarkan oleh matriks.

Apabila matriksnya berbentuk 2 × 2, maka rumus untuk mencari determinan ialah:

{\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}

Apabila matriksnya berbentuk 3 × 3 matrix A, maka rumusnya adalah:

{\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}

Rumus Leibniz untuk mencari determinan matriks n × n ialah:

$\det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right).$

Metode eliminasi Gauss juga bisa dipakai.

Sebagai contoh, yaitu pada determinan matriks berikut:

A={\begin{bmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{bmatrix}}

bisa dihitung dengan menggunakan sebuah matriks berikut:

B={\begin{bmatrix}-2&2&-3\\0&0&4.5\\2&0&-1\end{bmatrix}},\quad C={\begin{bmatrix}-2&2&-3\\0&0&4.5\\0&2&-4\end{bmatrix}},\quad D={\begin{bmatrix}-2&2&-3\\0&2&-4\\0&0&4.5\end{bmatrix}}.

Keterangan:

Di sini, B diperoleh dari A dengan menambahkan −1/2× baris pertama dengan baris yang kedua, sehingga det(A) = det(B).

Kemudian C diperoleh dari B dengan menambahkan kolom pertama dengan kolom ketiga, sehingga det(C) = det(B). Sementara itu, yang D didapat dari C dengan menukar kolom kedua dan ketiga, sehingga det(D) = −det(C). Determinan matriks segitiga D merupakan hasil dari perkalian diagonal utamannya : (−2) · 2 · 4.5 = −18.

Oleh karena itu, det(A) = −det(D) = +18.

Sifat – Sifat Determinan Matriks

Ada beberapa sifat – sifat determinan matriks, yaitu diantarannya:

1. Apabila semua elemen dari salah satu baris atau kolom sama dengan nol, maka determinan matriks tersebut adalah nol. Perhatikan contoh berikut:

Misalkan :

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

2. Apabila semua elemen dari salah satu baris atau kolom itu sama dengan elemen-elemen baris atau kolom lain, maka determinan matriks tersebut adalah nol.

Perhatikan contoh berikut:

Misalkan: B =

(Sebab elemen-elemen baris ke-1 dan ke-3 adalah sama).

3. Apabila elemen-elemen salah satu dari baris atau kolom adalah merupakan kelipatan dari elemen-elemen baris atau kolom lain maka determinan matriks tersebut adalah nol.

Perhatikan contoh di bawahberikut:

Misalkan: A =

(Sebab elemen-elemen baris ke-3 sama dengan kelipatan elemen-elemen baris ke-1).

4. |AB| : |A| ×|B|

5. |AT| = |A|, untuk AT ialah transpose dari matriks A.

6. |A^–1| =

, untuk A^–1 ialah invers dari matriks A.

7. |kA| = kn |A|, untuk A ordo n × n dan k adalahsuatu konstanta.

Contoh Soal dan Pembahasannya

Soal Determinan Ordo 2 x 2

Contoh 1:

Hitungalah dan Tentukan berapa nilai determinan dari sebuah matrik berikut :

Pembahasan:

M=

5	2
4	3

Jawab :

det(M) =

5	2
4	3

Maka = (5 × 3) – (2 × 4) = 7

Contoh 2:

Hitungalah dan Tentukan berapa nilai determinan dari matrik berikut :

Pembahasan:

N=

-6	-1
3	-2

Jawab:

det(N) =

-6	-1
3	-2

Maka = ((–6) × (-2)) – (3 × (–1)) = 15

Determinan Matriks Ordo 3 × 3

Misalnya kita ketahui sebuah matriks A, yang merupakan matriks persegi dengan ordo dua. Maka:

A=

a	b
c	d

Dengan demikian, dapat diperoleh sebuah rumus det A sebagai berikut:

det(A) =

a	b
c	d

Maka = ad – bc

Contoh 1:
Hitungalah dan Tentukan berapa nilai determinan dari matrik berikut :

M=

5	6
4	3

Pembahasan:

det(M) =

5	6
4	3

= (5 × 3) – (6 × 4) = 16

Contoh.2
Hitungalah dan Tentukan berapa nilai determinan dari matrik berikut :

N=

-6	-2
3	-2

Pembahasan:

det(N) =

-6	-2
3	-2

= ((–6) × (-2)) – (3 × (–2)) = 18

Determinan Matriks Ordo 3 × 3

Terdapat ada dua cara di dalam menghitung determinan untuk matriks berordo 3×3 ini, yaitu :

Metode Sarrus, dan
Metode Minor-Kofaktor

Cara yang paling mudah atau paling sering digunakan dalam menghitung suatu determinan matriks untuk yang berordo 3×3 yaitu metode Sarrus.

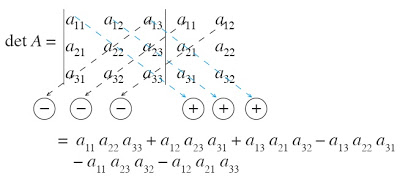
Metode Sarrus

Misalnya, kita mempunyai matriks A berordo 3×3 seperti berikut :

A =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

Maka cara perhitungan determinannya dapat ditunjukkan oleh gambar dibawah berikut:

Sekarang kita pelajari contoh berikut:

Contoh 1:
Tentukanlah Nilai Determinan dari matriks ordo 3×3 berikut :

A =

2	3	4
5	4	3
7	0	1

Pembahasan:

Nilai determinan untuk matriks di atas ialah sebagai berikut:

det(A) =

2	3	4
5	4	3
7	0	1

2	3
5	4
7	0

det(A) = 2.4.1 + 3.3.7 + 4.5.0 – 4.4.7 – 2.3.0 – 3.5.1 = 8 + 63 + 0 – 112 – 0 – 15 = – 56

Contoh 2:
Tentukanlah Nilai Determinan dari matriks ordo 3×3 berikut :

B =

1	2	3
2	1	4
3	1	2

Pembahasan:

Nilai determinan untuk matriks di atas ialah sebagai berikut:

det(B) =

1	2	3
2	1	4
3	1	2

1	2
2	1
3	1

det(A) = (1.1.2) + (2.4.3) + (3.2.1) – (3.1.3) – (1.4.1) – (2.2.2) = 2 + 24 + 6 – 9 – 4 – 8 = 11

Demikianlah pembahasan kita mengenai Determinan Matriks. Semoga bermanfaat …

Artikel Lainnya:

Pengertian Determinan Matriks

Sifat – Sifat Determinan Matriks

Contoh Soal dan Pembahasannya

Soal Determinan Ordo 2 x 2

Contoh 1:

Hitungalah dan Tentukan berapa nilai determinan dari sebuah matrik berikut :

Pembahasan:

M=

Jawab :

det(M) =

Maka = (5 × 3) – (2 × 4) = 7

Pembahasan:

N=

det(N) =

Maka = ((–6) × (-2)) – (3 × (–1)) = 15

Determinan Matriks Ordo 3 × 3

A=

det(A) =

Maka = ad – bc

M=

Pembahasan:

det(M) =

= (5 × 3) – (6 × 4) = 16

N=

Pembahasan:

det(N) =

= ((–6) × (-2)) – (3 × (–2)) = 18

Determinan Matriks Ordo 3 × 3

Metode Sarrus

A =

A =

det(A) =

B =

det(B) =

Share this: