Gerak Parabola- Definisi, Komponen, Rumus dan Contoh Soalnya- Hallo sahabat, kali ini kami akan berbagi ilmu mengenai Gerak Parabola- Apa itu gerak para bola? Bagaiana definisinya? Apa komponen-komponennya? Adakah rumus dan Contoh Soalnya.

Untuk lebih jelasnya, langsung saja yuk kita simak!

Gerak Parabola juga dikenal sebagai Gerak Peluru. Kenapa dinamakan Gerak parabola? karena lintasannya berbentuk parabola, bukan bergerak lurus.

Contoh bentuk gerak parabola ini dapat kita lihat pada gerakan bola saat dilempar, gerakan pada peluru meriam yang ditembakkan, gerakan pada benda yang dilemparkan dari pesawat dan gerakan pada seseorang yang melompat maju.

Daftar Isi Artikel :

Definisi Gerak Parabola

Gerak parabola dapat didefinisikan yaitu sebuah gerak dua dimensi pada suatu benda yang bergerak membentuk sudut elevasi dengan sumbu x atau sumbu y. Sumbu x (horizontal) adalah GLB dan sumbu y (vertikal) adalah GLBB.

Kedua gerak ini tidak saling mempengaruhi, hanya saja membentuk suatu gerak parabola.

Perhatikan gambar berikut:

Dari gambar diatas dapat disimpulkan, bahwa terdapat 3 titik yang mengandung keterangan sebagai berikut:

Pada titik A, merupakan titik awal gerak suatu benda. Benda memiliki kecepatan awal $(V_0)$ .

Pada titik B, benda berada di akhir lintasannya.

Pada titik C, merupakan titik tertinggi suatu benda. Benda berada pada sebuah ketinggian maksimal $(y_{maks})$ , pada titik ini kecepatan vertikal benda besarnya 0 (nol) ( $V_{y \: di \: titik \: C} = 0$ )

Komponen Gerak Parabola Dan Rumusnya

Gerak parabola yang merupakan gerak gabungan dari dua komponen gerak yaitu terdiri atas komponen gerak horizontal (sumbu x) dan komponen gerak vertikal (sumbu y).

Mari kita bahas kedua komponen tersebut:

Komponen gerak parabola sisi horizontal (pada sumbu X): $(V_x)$
1. Komponen gerak horizontal besarnya selalu tetap dalam setiap rentang waktu karena tidak terdapat percepatan maupun perlambatan pada sumbu x $a_x = 0$ , Maka:
  $V_x = V_{x0} = V_{xt} = \: konstan$
2. Terdapat sudut (θ) antara kecepatan benda (V) makan dengan komponen gerak horizontal $V_x$ dalam setiap rentang waktu, maka:
  $V_x = V_{x0} = V_{xt} = V_0 \cos \theta_0$
3. Karena tidak terdapat percepatan maupun perlambatan pada sumbu X, maka untuk mencari jarak yang ditempuh benda (x) pada selang waktu (t) dapat kita hitung dengan rumus sebagai berikut:
  $rumusbilangan$
Komponen gerak parabola sisi vertikal (pada suatu sumbu y): $V_y$
1. Komponen gerak vertikal besarannya selalu berubah dalam setiap rentang waktu karena benda tersebut dipengaruhi oleh percepatan gravitasi (g) pada sumbu y. Maka kamu harus pahami bahwa benda mengalami perlambatan akibat gravitasi $a_y = -g$
2. Terdapat sudut [θ] antara kecepatan suatu benda (V) dengan komponen gerak vertikalnya $(V_y)$ , maka:
  $V_y = V_0 \sin \theta_0 - gt$
3. Karena dipengaruhi percepatan gravitasi, maka komponen gerak vertikal $(V_y)$ pada selang waktu (t) tertentu dapat kita cari dengan rumus:
  $V_y = V_0 \sin \theta_0 - gt$
4. Kita dapat mencari ketinggian suatu benda (y) pada selang waktu (t) dengan menggunakan rumus:
  $y = V_0 \sin \theta_0 \cdot t - \frac{1}{2} g t^2$
Terdapat pula persamaan-persamaan untuk menentukan suatu besaran gerak parabola lainnya, yaitu:
1. Apabila tidak diketahui komponen waktu, kita bisa dapat langsung mencari jarak tempuh benda terjauh ( $x_{max}$ ), yakni dari titik A hingga ke titik B, dengan menggabungkan kedua komponen gerak.
  Komponen gerak horizontal yaitu:
  $x_{max}=V_{max} \times t_{max}$
  Komponen gerak vertikal yaitu:
  $t_{di \: titik \: C} = V_{y0} / g$
  Dengan mensubstitusikan kedua persamaan diatas, maka kita telah mendapatkan persamaan:
  $x_{max} = (V_0^2 \sin 2 \theta_0) / g$
2. Kita dapat pula langsung menghitung ketinggian benda maksimum $(y_{max})$ dengan persamaan:
  $y_{max} = V_0^2 \sin^2 \theta_0 / 2g$
3. Selain itu, dengan menggunakan teorema Pythagoras kita dapat mencari kecepatan benda jika kedua komponen lainnya diketahui.
  $V= \sqrt{V_x^2 + V_y^2}$
4. Apabila diketahui kedua komponen kecepatan, kita juga dapat mengetahui besarnya sudut θ yang dibentuk, yaitu: $\tan \theta = V_y / V_x$

Contoh Soal Gerak Parabola

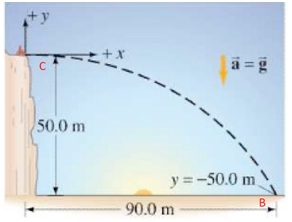
Seorang Peraga pengganti melaju mengendarai sepeda motor menuju ujung tebing setinggi 50 m.
Berapakah kecepatan yang harus dicapai motor tersebut saat melaju dari ujung tebing menuju kelandasan dibawahnya sejauh 90 m dari tebing? Dari sini kita abaikan gesekan udaranya.

Pembahasannya:

Kita gambar terlebih dahulu lintasan gerak parabola objek tersebut. Maka kurang lebih akan tergambar sebuah gambar seperti dibawah berikut:

Kemudian setelah kita gambar dan perhatikan, sekarang kita identifikasi komponen-komponen yang terdapat dalam gambar tersebut:

$x_{max} = 90 m \qquad a_x = 0 \qquad y_c = y_0 = 0 \newline \newline a_y = -g = - 9,8 m/s^2 \qquad y_b = -50$ m.

$V_{y0} = 0$ ,

maka selanjutnya kita tahu bahwa $V_{x0} = V_0$

Dengan menggunakan rumus untuk mencari ketinggian benda, maka kita bisa mendapatkan waktu tempuhnya yaitu sebagai berikut:

$y = V_{y0} t - \frac{1}{2} gt^2 \newline \newline y = 0 - \frac{1}{2} gt^2 \newline \newline y = - \frac{1}{2} gt^2 \newline \newline t^2 = \frac{2y}{-g} \Longrightarrow t = \sqrt{\frac{2y}{-g}} = \sqrt{\frac{2 (-50 m)}{- 9,8 m/s^2}} \newline \newline t = 3,19 s$

Dengan rumus untuk mencari jarak tempuh, kita bisa mendapatkan kecepatan motor dengan rumusnya:

$x = V_{x0} \times t \newline \newline V_{x0} = \frac{x}{t} = \frac{90 m}{3.19 s} = 28,21 \: m/s$ .

Maka hasilnya, kecepatan yang harus dicapai motor tersebut yaitu harus sebesar 28,21 m/s atau sekitar 100 km/h (101,55 km/h).

Demikianlah pembahasan kita pada hari ini mengenai gerak parabola. Semoga bermanfaat ya…

Baca Juga:

Definisi Gerak Parabola

Komponen Gerak Parabola Dan Rumusnya

Komponen gerak parabola sisi horizontal (pada sumbu X): <img class="latex alignnone" title="(V_x)" src="../latex.php-latex-(V_x)-bg-f9f9f9-fg-000000-s-0.jpg" alt="" width="27" height="18"/>

Komponen gerak parabola sisi vertikal (pada suatu sumbu y):

Terdapat pula persamaan-persamaan untuk menentukan suatu besaran gerak parabola lainnya, yaitu:

Contoh Soal Gerak Parabola

Share this:

Related posts:

Komponen gerak parabola sisi horizontal (pada sumbu X): $(V_x)$

Komponen gerak parabola sisi vertikal (pada suatu sumbu y): $V_y$